
פונקציה רציפה (אנליזה)
ויקיפדיה האנציקלופדיה encyclopedia
בחשבון אינפיניטסימלי, רְצִיפוּת היא תכונה של פונקציה ממשית. נאמר על פונקציה שהיא רציפה אם לכל נקודה בתחום הגבול שווה לערך הפונקציה באותה נקודה. באופן אינטואיטיבי, פונקציה רציפה היא פונקציה שאפשר לצייר את הגרף שלה מבלי להרים את העיפרון מהדף.

בערך זה |

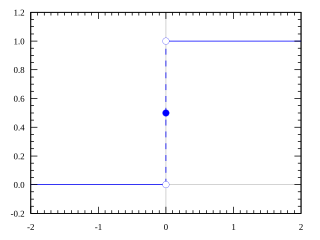

רציפות היא תנאי הכרחי לגזירות, אך לא תנאי מספיק. בנוסף, כל פונקציה אלמנטרית היא פוקנציה רציפה בתחום הגדרתה.
רעיונות דומים מופיעים באופן כללי יותר במרחבים מטריים ואפילו מרחבים טופולוגיים כלליים, ראו: רציפות (טופולוגיה).